范畴学基本知识

范畴学（category theory）是数学中的一个抽象分支，能够形式化诸如集合论（set theory）、类型论（type theory）、群论（group theory）以及逻辑学（logic）等数学分支中的一些概念。范畴学主要处理对象（object）、态射（morphism）和变化式（transformation），而这些概念跟编程的联系非常紧密。下图是一些相同的概念分别在不同理论下的形式：

在范畴学中，有一个概念叫做…范畴。有着以下这些组件（component）的搜集（collection）就构成了一个范畴：

• 对象的搜集
• 态射的搜集
• 态射的组合
• identity 这个独特的态射

对象的搜集

对象就是数据类型，例如 String、Boolean、Number 和 Object 等等。通常我们把数据类型视作所有可能的值的一个集合（set）。像 Boolean 就可以看作是 [true, false] 的集合，Number 可以是所有实数的一个集合。把类型当作集合对待是有好处的，因为我们可以利用集合论（set theory）处理类型。

态射的搜集

态射是标准的、普通的纯函数。

态射的组合

compose 函数是符合结合律的，这并非巧合，结合律是在范畴学中对任何组合都适用的一个特性。

这张图展示了什么是组合：

1
2
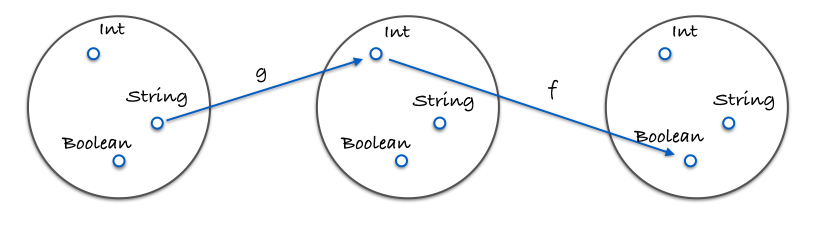
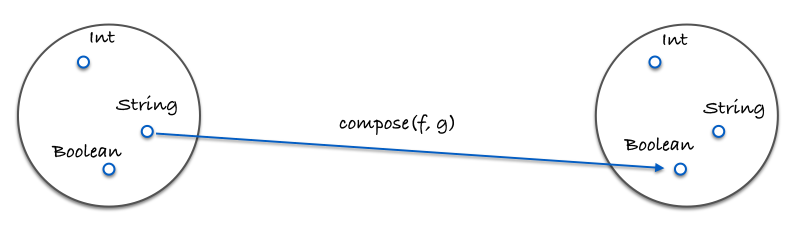
3

var g = function(x){ return x.length; };
var f = function(x){ return x === 4; };
var isFourLetterWord = compose(f, g);

identity 这个独特的态射

让我们介绍一个名为 id 的实用函数。这个函数接受随便什么输入然后原封不动地返回它：

1

var id = function(x){ return x; };

除了类型和函数，还有什么范畴呢？还有很多，比如我们可以定义一个有向图（directed graph），以节点为对象，以边为态射，以路径连接为组合。还可以定义一个实数类型（Number），以所有的实数对象，以 >= 为态射（实际上任何偏序（partial order）或全序（total order）都可以成为一个范畴）。

命令式编程 和 申明式编程 区别

1
2
3
4
5
6
7
8
9

// 命令式
var makes = [];
for (i = 0; i < cars.length; i++) {
  makes.push(cars[i].make);
}


// 声明式
var makes = cars.map(function(car){ return car.make; });

1
2
3
4
5
6
7
8

// 命令式
var authenticate = function(form) {
  var user = toUser(form);
  return logIn(user);
};

// 声明式
var authenticate = compose(logIn, toUser);

声明式代码不指定执行顺序，所以它天然地适合进行并行运算。它与纯函数一起解释了为何函数式编程是未来并行计算的一个不错选择——我们真的不需要做什么就能实现一个并行／并发系统。